ASAC 빅데이터 분석가 7기/DL(Deep Learning)
FNN (Feedforward Neural Network) 순방향 신경망
junslee
2025. 2. 10. 16:42
FNN (Feedforward Neural Network) 순방향 신경망
- FNN은 데이터 구조에 대한 특별한 가정사항 없는 가장 기본이 되는 신경망
- 데이터가 한 방향으로 전달되는 연결 구조만을 갖는 구조

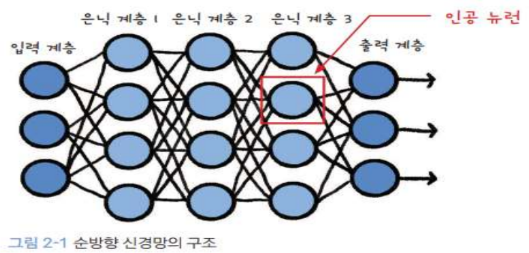
FNN 구조
- 뉴런들이 모여 계층을 이루고 -> 이 계층이 쌓여 전체적인 신경망을 이루는 구조
- Input Layer + Hidden Layer + Output Layer
- Hidden Layer의 복잡도에 따라서 가변적으로 구성된다.
- 입력층(Input Layer)
입력 데이터를 받는 계층
입력 노드의 개수는 모델에 전달된 데이터의 특성(feature) 수와 동일하다. - 은닉층(Hidden Layer)
입력 데이터에서 패턴을 학습하는 계층
이 계층에서는 가중치(weight)와 편향(bias)을 기반으로 데이터를 비선형적으로 변환하는 과정을 거친다.
여러 개의 은닉층을 사용할 수 있으며, 층의 개수와 노드 수는 모델 설계에 따라 유동적이다.
활성화 함수(Activation Function)가 적용되어 데이터를 변형하거나 출력값에 비선형성을 부여한다. - 출력층(Output Layer)
모델의 최종 예측값을 생성하는 계층
회귀 문제에서는 연속적인 값, 분류 문제에서는 클래스 확률 또는 예측 클래스가 출력된다.
출력층에서도 문제 유형에 따라 적절한 활성화 함수가 사용된다.(예: softmax, sigmoid 등).
- FCL 연결
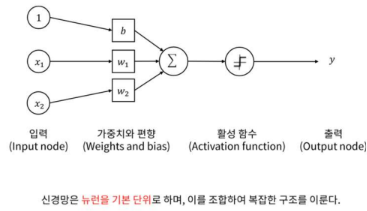
- 뉴런 Neuron
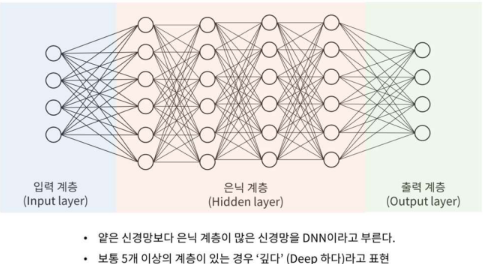
- 얕은 신경망 Shallow Neural Network

- 심층 신경망 Deep Neural Network (DNN)
FNN의 작동 원리
- 1. 입력 데이터 전달
입력 데이터를 입력층에 전달한다. - 2. 가중치와 편향 계산
각 계층의 노드들은 입력 데이터와 가중치를 곱하고 편향을 더한 합을 계산한다.
z=Wx+b
W : 가중치 행렬
x : 입력 값
b : 편향 벡터
- 3.활성화 함수 적용
위에서 계산된 z에 활성화 함수(예: ReLU, Sigmoid, Tanh 등)를 적용하여 비선형성을 추가한다.
활성화 함수는 모델이 복잡한 패턴을 학습할 수 있도록 한다.
a=f(z)
: 활성화 함수
a: 활성화 함수 출력 값
- 4. 출력층 전달
은닉층에서 전달된 데이터를 출력층으로 보내 최종 예측을 수행한다. - 5. 손실 계산
모델의 출력값과 실제 정답 값을 비교하여 손실 함수(Loss Function)를 계산한다.
이 손실 값은 모델의 성능을 평가하는 데 사용된다. - 6. 역전파(Backpropagation)
손실 값을 기반으로 가중치와 편향을 업데이트한다.
경사하강법(Gradient Descent)과 같은 알고리즘을 사용하여 가중치를 최적화한다.
FNN에서는 역전파 알고리즘이 필수적으로 사용된다.
활성화 함수 (Activation Function)
FNN에서는 활성화 함수가 중요한 역할을 한다.
활성화 함수는 은닉층 또는 출력층에서 계산된 값을 변형하여 모델에 비선형성을 부여한다.
- Sigmoid: 출력 값을 [0, 1] 범위로 압축. 주로 출력층에서 사용.
특징:
출력이 확률처럼 사용될 수 있습니다.
주로 출력층(이진 분류)에서 사용됩니다.
장점:
값이 0에서 1 사이로 제한되어 확률 해석이 가능.
단점:
기울기 소실 문제(Vanishing Gradient): 입력이 극단적인 경우(아주 크거나 작을 때), 기울기가 거의 0이 되어 학습이 잘 이루어지지 않습니다.
출력값이 0 또는 1에 가까워질수록 뉴런 업데이트가 어려워집니다.
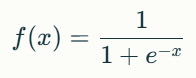
- ReLU(Rectified Linear Unit): 음수 값을 0으로 만들고, 양수는 그대로 유지. 딥러닝에서 많이 사용.
특징:
계산이 간단하며 학습 속도가 빠릅니다.
대부분의 딥러닝 모델에서 기본 활성화 함수로 사용됩니다.
장점:
기울기 소실 문제(Vanishing Gradient)를 완화.
음수를 0으로 만들어 Sparse Activation(희소 활성화)을 가능하게 함.
단점:
죽은 ReLU 문제(Dead Neurons)
입력값이 항상 0보다 작으면 가중치가 업데이트되지 않아 뉴런이 "죽은 상태"가 됩니다.

- Tanh: 출력 값을 [-1, 1] 범위로 압축. Sigmoid보다 더 강력한 비선형성을 제공.
특징:
Sigmoid 함수와 유사하지만 출력값이 중앙(0)을 기준으로 하여 더 대칭적입니다.
장점:
Sigmoid 함수보다 출력값이 넓은 범위를 가지므로 학습이 더 잘 이루어질 수 있습니다.
단점:
기울기 소실 문제 발생 가능.
입력값이 극단적일 경우, Sigmoid와 유사하게 기울기가 0에 가까워질 수 있습니다.

- Softmax: 분류 문제에서 클래스 확률 계산을 위해 사용. 출력이 확률 분포를 형성.
특징:
주로 다중 클래스 분류 문제의 출력층에서 사용됩니다.
각 클래스의 확률 분포로 변환하므로 예측 결과를 확률로 해석할 수 있습니다.
장점:
직관적인 확률 해석을 제공.
여러 클래스 간 상호작용을 고려.

- Swish: 입력값과 Sigmoid 값을 곱한 형태의 활성화 함수
특징:
ReLU나 Sigmoid보다 더 나은 성능을 보이는 경우가 많습니다.
Smooth(부드러운) 비선형 특성을 가집니다.
장점:
ReLU와 달리 음수 값도 일정 부분 학습에 기여할 수 있습니다.
단점:
다른 함수들에 비해 계산량이 많습니다.

FNN(특징추출) 뉴런 구조
- 뉴런은 데이터에 내재한 특징을 추출하기 위해 가중치가 있는 선형결합을 입력으로 하여 Activation Function(활성화 함수)를 바탕으로 다음으로 넘겨준다.
- Activation Function은 "Non-Linear"인 비선형적인 함수를 사용하여 비선형을 활용할 수 있게 함

“선형결합” - 비선형성을 추가하기 위한 전처리 단계
- 선형결합은 비선형성을 추가하기 전에 데이터를 변환하는 기본 단계이다.
- 데이터를 직선이나 평면으로 표현하지만, 여기에 활성화 함수(예: Sigmoid, ReLU 등)를 적용하면 데이터에 비선형성이 추가된다.
- 신경망은 단순히 선형적인 문제뿐만 아니라 복잡한 패턴과 관계를 학습할 수 있다.
- 선형결합의 목적은 데이터를 중요한 패턴에 따라 가중치를 조정하고, 문제를 수학적으로 표현할 기반을 제공한다.
비선형 활성화 함수(Non-linear Activation Function)
- 딥러닝 모델에서 입력값(선형 결합의 결과)을 비선형적으로 변환하는 함수
- 경망에서 활성화 함수는 비선형성을 추가하여 단순한 선형 모델로는 해결할 수 없는 복잡한 문제를 학습할 수 있도록 한다.
- 활성화 함수의 선택 기준
ReLU: 기본적으로 대부분의 은닉층에서 사용. 계산이 빠르고 기울기 소실 문제를 완화.
Sigmoid: 출력층에서 확률값 해석이 필요한 이진 분류 문제에서 사용.
tanh: 은닉층에서 사용 가능하며, Sigmoid보다 학습이 잘 이루어짐.
Softmax: 다중 분류 문제의 출력층에서 사용.
Leaky ReLU / Swish: Dead ReLU 문제를 해결하거나 더 나은 성능을 원할 때 사용.
- 비선형 활성화 함수의 핵심 목표는 비선형성을 도입하여 신경망이 복잡한 패턴과 관계를 학습할 수 있도록 하는 것이다.
FNN의 기능
신경망(FNN: Feedforward Neural Network)이 어떻게 수학적으로 합성함수(Composite Function)로 볼 수 있는지, 그리고 이것이 범용 함수 근사(Universal Approximation) 기능과 어떻게 연결되는지
- 1. 뉴런: 실함수의 역할
뉴런의 역할과 정의:
신경망에서 개별 뉴런(Neuron)은 입력값에 대한 선형결합과 비선형 변환을 수행하는 가장 작은 단위이다.
뉴런 단위에서는 단일 실수 값을 출력 (스칼라 출력)
활성화 함수 f를 통해 비선형성을 추가하여 단순 선형 모델의 한계를 극복
뉴련의 계산 공식:
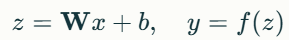

- 뉴런은 선형결합을 한 뒤, 활성화 함수를 적용하여 비선형 변환을 수행하는 실함수(Real-valued Function)로 볼 수 있다.
- 2. 계층(Layer): 벡터 함수의 역할
계층의 역할:
계층(Layer)은 여러 뉴런으로 구성된 모듈로, 입력 벡터를 벡터 함수(Vector Function)로 변환한다.
각 뉴런마다 입력 벡터 x를 처리하고, 계산 결과는 하나의 벡터로 출력된다.
계층의 의미:
벡터 함수
가중치 공유 및 병렬 계산
계층의 수학적 표현:
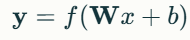

- 3. 신경망(Neural Network): 벡터 함수들의 합성
신경망의 역할:
신경망(FNN)은 여러 계층을 순차적으로 쌓아 올린 구조로 하나의 큰 합성함수(Composite Function)로 볼 수 있다.
각 계층이 벡터 함수를 정의하며, 이들이 연결되면서 최종적으로 전체 신경망은 입력을 출력으로 변환하는 복잡한 함수로 표현된다.
신경망의 의미:
계층적 특징 학습
복잡한 함수 모델링
신경망의 수학적 표현:
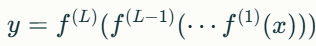

- 4. 범용 함수 근사(Universal Approximation Theorem)
범용 함수 근사의 역할:
충분히 많은 뉴런과 은닉층을 가진 신경망(심층 신경망 또는 다층 퍼셉트론)은 어떠한 연속적인 함수라도 원하는 정도의 정확도로 근사할 수 있다.
임의의 연속 함수 f와 임의의 작은 오차 ϵ>0에 대해, 적절한 구조(뉴런 수와 가중치)를 가진 심층 신경망 g가 존재하여 다음을 만족한다.
범용 함수 근사의 의미:
신경망은 복잡한 데이터 관계나 함수(심지어 비선형적이고 고차원적인 관계)를 학습 또는 근사할 수 있다.
층(Layer)이 많아질수록 더 복잡한 패턴을 학습할 수 있다.
범용 함수 근사의 수학적 표현:
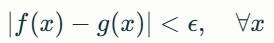
실함수, 벡터 함수, 신경망의 관계
신경망의 계층적 구성 요약
- 뉴런 (실함수 ):
- 가장 작은 단위.
- 선형결합과 활성화 함수 적용을 통해 스칼라 값을 출력하는 실함수.
- 계층 (벡터 함수 f):
- 뉴런의 집합으로, 입력 벡터 를 또 다른 벡터 y로 변환.
- 벡터에 대한 선형 변환(가중치 행렬 곱) + 비선형 활성화 함수 적용.
- 신경망 (합성 함수 ):
- 여러 계층(벡터 함수)을 합성하여, 입력 를 최종 출력 로 매핑.
- 전체 신경망은 하나의 복잡한 벡터 함수.
계층적 함수의 역할
- 뉴런: 데이터를 개별적으로 처리하여 작은 단위를 계산.
- 계층: 뉴런의 출력을 결합하여 고차원적인 벡터 변환 수행.
- 신경망: 계층의 결과를 합성하여 입력-출력 간의 복잡한 관계를 모델링.
- 뉴런 실함수: 신경망의 가장 작은 계산 단위로, 입력과 가중치의 선형결합 후 활성화 함수 적용.
- 계층 벡터 함수: 여러 뉴런으로 구성된 벡터 함수로, 입력 데이터를 선형 변환 + 비선형 변환.
- 신경망 합성 함수: 여러 계층(벡터 함수)을 합성하여 입력 데이터를 출력으로 매핑하는 복잡한 함수.
범용 함수 근사와의 연결
신경망이 이러한 계층적 구조를 통해 데이터를 처리하기 때문에, 충분한 뉴런과 계층을 활용하면 복잡한 연속 함수를 학습할 수 있는 범용 함수 근사 기법으로 작동한다.
이를 통해 신경망은 패턴 인식, 예측, 분류 등 다양한 문제에서 뛰어난 성능을 발휘할 수 있다.
실전 문제에 적용 - 분류 문제
Binary Classification
- 정의: 데이터가 두 개의 클래스로 구분되는 문제다.
예를 들어, 이메일이 스팸인지 아닌지를 분류하거나, 환자가 특정 질병에 걸렸는지 여부를 판단하는 문제가 이에 해당한다. - 활성화 함수: 출력 노드에서 예측값을 확률로 변환하기 위해 Sigmoid 함수를 사용한다.
Sigmoid 함수는 입력값을 (0,1) 범위로 매핑하며, 확률로 해석할 수 있다.
이를 통해 모델의 출력값을 특정 클래스에 속할 가능성으로 이해할 수 있다.

- 출력값이 0.5보다 크면 클래스 1로, 작으면 클래스 0으로 분류하는 방식으로 활용된다.
- 특징:
Sigmoid 함수는 확률값을 제공하여 비교와 해석이 용이하다.
Binary Cross-Entropy 손실 함수를 함께 사용하여 모델 학습을 최적화한다.
Multi-Classification
- 정의: 데이터가 세 개 이상의 클래스로 나뉘는 문제다.
예를 들어, 사진 속 동물이 고양이, 개, 새 중 어느 것인지 분류하는 문제가 이에 해당한다. - 활성화 함수: 여러 클래스에 대한 확률값을 제공하고, 이들의 합이 1이 되도록 보장하기 위해 SoftMax 함수를 사용한다.

클래스 i에 대한 로짓(logit) 값
K는 전체 클래스의 수
- SoftMax는 각 클래스에 대해 확률 분포를 생성하며, 가장 높은 확률값을 가진 클래스를 예측 결과로 선택한다.
- 특징:
SoftMax는 다중 클래스 간의 상호작용을 고려하여 확률을 계산한다.
Multinomial Cross-Entropy 손실 함수를 사용하여 모델 학습을 최적화한다.
실전 문제에 적용 - 회귀 문제
- 정의
회귀 문제는 연속적인 값을 예측하는 문제다.
예를 들어, 주택 가격이나 주식 시장의 변동을 예측하는 경우가 이에 해당된다. - 활성화 함수
회귀 문제에서는 출력값을 변형하지 않고 그대로 사용하는 것이 중요하다.
이를 위해 **항등 함수(Identity Function)**를 활성화 함수로 사용한다. (항등 함수 : f(x) = x)
항등 함수는 출력값이 실수 범위 전체를 포함할 수 있도록 보장하며, 이는 연속적인 값을 다루는 회귀 문제에서 필수적이다. - 특징
항등 함수는 비선형성을 추가하지 않으므로, 모델의 출력이 입력 특징과 선형적으로 연결될 수 있다.
손실 함수로 주로 Mean Squared Error(MSE)를 사용하여 예측값과 실제값 간의 차이를 최소화하도록 학습한다.
FNN Activation Function

ReLU : Rectified Linear Unit

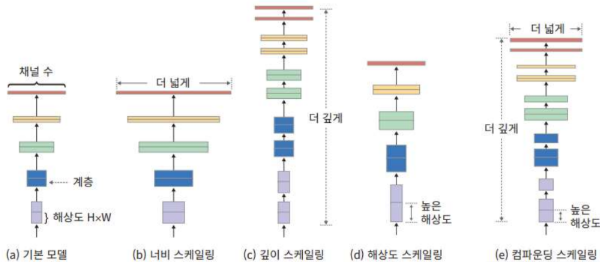
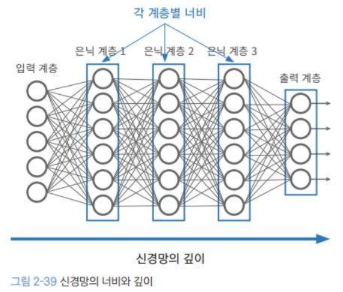
FNN : Depth & Width
- 신경망의 모델의 크기 : 너비 & 깊이
너비 : 계층에 들어 있는 뉴런의 수
깊이 : Layer의 수
- 특징이 많고 데이터간의 관계가 복잡하면
-> 특징 학습에 관련된 뉴런의 수 증가하도록 설계
-> 절대치는 없어서, 경험 & 유사 모델 성능을 기반으로 하게 된다. - ML에서 사용한 Gridsearch & RandomGridSearch 등과 같은 방식도 사용함~ -> 최근 NAS(Network Architecture Search)
- 일반적인 접근 방식 : 성능이 좋다고 검증된 모델 선택 -> 나의 문제에 맞게 거기서 수정