ASAC 빅데이터 분석가 7기/ASAC 일일 기록
ASAC 빅데이터 분석가 과정 44일차 (25.02.12)
junslee
2025. 2. 12. 09:19
Learning~
비선형 함수의 최적화 문제
intro
- Cost Function의 값을 최소/최대화를 하는 W를 찾자 -> 최적화 문제

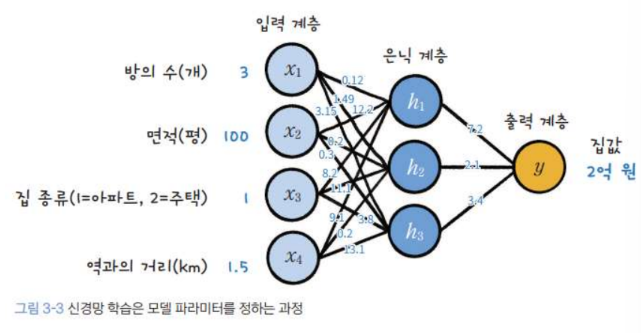
최적화의 표현
- 결국, “Loss Function”에 대한 최소를 하는 “파라미터의 최적화“ 를 해야 하는 문제
- 어디서 출발을 하느냐에 상관없이 최적의 장소에 도달하고자 해야 한다.

최적화의 표현 : 분류
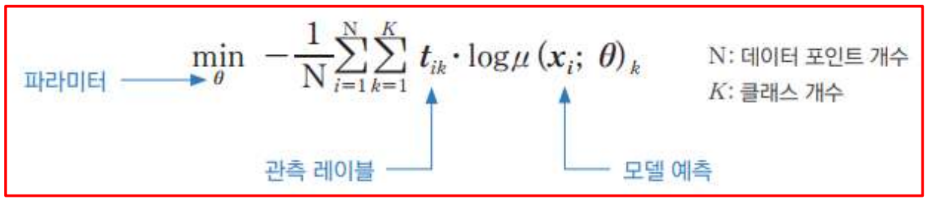
최적화의 표현 : 회귀
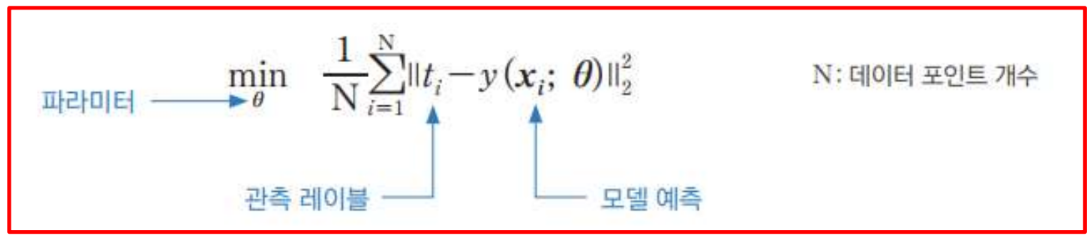
최적의 값을 어떻게 찾지?
- 신경망의 최적화 알고리즘의 기본은 경사하강법 Gradient Descent 에서 출발한다.
-> 최근에는 이를 기반으로 확장& 변형된 방법이 있다. - 간단히 왜 이론적으로 처음에 Gradient Descent가 제시가 되었고, 어떠한 특징이 있는지 알아보려고 한다.
- 기본적으로 어디서 출발을 해도 Local Min에 빠지지 않고, Global Min에 도달하고자 한다
- 실제는 Parameter의 수가 엄청 많아서 엄청나게 큰 차원에서 찾아야 한다

- 일반적인 최적화 문제의 문제
- 관측 변수가 많다.
- 닫힌 형태로 정의 되지 않는다. (Ridge Regresstion과 같은)
-> 함수에 대한 미분을 통한 최대/최소를 구할 수 없다.
=> 임의의 값에서 출발(초기값)해서 반복적으로 조금씩 접근하는 근사적인 수치해석적인 접근으로 하게 되어야 한다. - 2차 미분 : 곡률을 사용해서 최적의 해를 빨리 찾을 수 있다.
-> 손실함수가 Convex로 굴곡이 있어야 가능하다. (계산 비용과 메모리 사용량이 많음) - 1.5차 미분 : 1차 미분을 활용하여 2차 미분에 대한 근사로 접근
-> 2차 미분을 근사하는 알고리즘으로 수행 (메모리 사용량이 많음) - 1차 미분 : 수렴 속도가 상대적으로 느림 -> 손실함수가 꼭 Convex 형태일 필요 없음 -> 복잡한 Loss Function에서 어떠한 모양이 될 지 모를 떄 유용
- 결론) 1차 미분을 기본으로 하는 경사하강법 Gradient Descent를 기본으로 한 것을 주로 활용

Gradient Descent
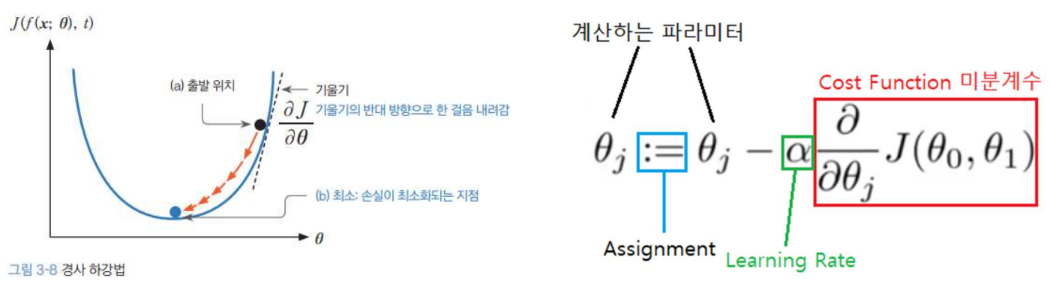
- 변수가 여러가지(파라미터가 여러개)인 경우 Vector로 표현
-> 각 성분별 편미분 사용

Gradient Descent : 2 Layers Regression
- 2 layer 구성
Activation Function -> ReLU
Regresstion -> Activation : Identity
Loss Function -> J(y,t) : MSE

- 합성함수를 미분하기 위해서 Chain Rule 사용

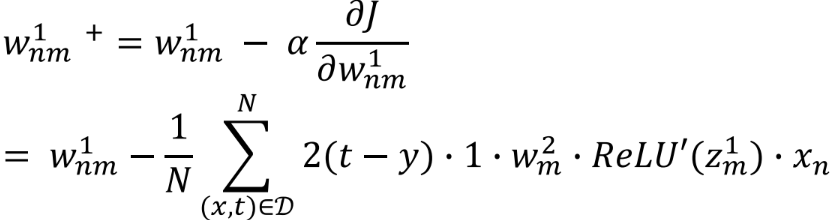
-> 신경망의 모든 파라미터에 미분의 연쇄 법칙을 적용해서 경사하강법을 적용할 수 있다.
- 인공 신경망(ANN)에서 Gradient Descent를 적용할 때, Loss function에서 부터 시작하여서 각 Layer들을 역방향으로 접근하며, 지금까지 실행했던 함수들을 역으로 따라가며, 미분값을 곱하며 연산한다.
-> 파라미터 수가 엉청 많다.
=> 반복을 엉청나게 많이 하는 비효율 발생

Back Propagation
- Loss Function 미분

- Output Layer 미분

- Hidden Layer 미분

- 뉴런 관점
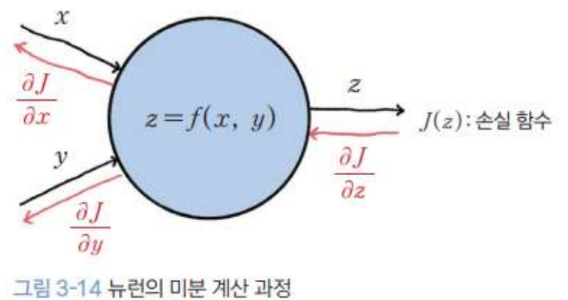

- Layer 단위 미분
- 뉴런에서는 vector로
신경망 학습과 최적화 알고리즘
1. 신경망 학습의 기본 개념
- 모델 파라미터: 신경망의 가중치와 편향은 모델의 주요 파라미터로, 학습 과정에서 최적화됩니다.
- 학습의 목표: 손실 함수(Loss Function)를 최소화하여 최적의 파라미터 값을 찾는 것입니다.
- 최적화 문제: 일반적으로 비선형 함수의 최적화를 다루며, 제약 조건이 있는 경우도 포함됩니다.
2. 최적화 알고리즘
Gradient Descent (경사하강법)
- 기본 원리: 손실 함수의 기울기를 계산해 점진적으로 최소값(Global Minimum)에 도달합니다.
- 변형된 방법들:
- 1차 미분 기반: 단순하고 복잡한 손실 함수에서도 사용 가능.
- 1.5차 미분 기반: 2차 미분을 근사하여 빠르게 접근하지만 메모리 소모가 큼.
- 2차 미분 기반: 곡률 정보를 활용해 빠르게 수렴하지만 계산 비용이 높음.
Gradient Descent의 변형 알고리즘
- SGD (Stochastic Gradient Descent): 데이터 샘플 단위로 경사를 계산하여 빠르지만 진동이 큼.
- Mini-Batch Gradient Descent: 데이터 일부를 묶어 학습하며, 속도와 안정성 간 균형을 유지.
- Batch Gradient Descent: 전체 데이터를 사용해 경사를 계산하지만 메모리 소모가 큼.
3. Backpropagation (역전파)
- 개념: 손실 함수에서 시작하여 각 층(layer)을 역방향으로 따라가며 기울기를 계산합니다.
- Chain Rule 활용:
- 손실 함수의 미분값을 각 층에 전달하며, 가중치와 편향에 대한 기울기를 계산.
- 공통 계산 부분은 재사용하여 효율성을 높임.
- 뉴런 단위와 레이어 단위 미분:
- 뉴런 단위에서는 벡터로, 레이어 단위에서는 행렬(Jacobian Matrix)로 확장.
4. 활성 함수와 손실 함수
- 활성 함수(Activation Function): ReLU, Identity 등 사용.
- 손실 함수(Loss Function): 회귀 문제에서는 평균제곱오차(MSE)를 주로 사용.
5. 데이터셋 구성 및 학습 방식
데이터셋 분할
- 훈련 데이터(Training Set), 검증 데이터(Validation Set), 테스트 데이터(Test Set)로 나뉩니다.
훈련 데이터 단위
- Batch 방식: 전체 데이터를 사용해 부드러운 경로로 학습.
- Mini-Batch 방식: 일반적으로 사용되며, 작은 데이터 묶음으로 학습해 일반화 성능을 높임.
- Stochastic 방식: 샘플 단위로 학습하며 진동이 크지만 메모리 효율적.
6. Optimizer (최적화 기법)
Adagrad
- 과거 기울기 정보를 활용해 변수별 학습률을 조정.
- 단점: 누적된 기울기로 인해 학습이 멈출 수 있음.
RMSprop
- 지수 이동 평균을 사용해 Adagrad의 문제를 개선.
- 기울기 변화가 큰 경우에도 안정적으로 작동.
Adam
- SGD 모멘텀과 RMSprop을 결합한 방식.
- 관성과 적응적 학습률을 동시에 활용하여 빠르고 안정적인 수렴을 보임.
- 초기 경로 편향 문제를 보정하는 추가 단계 포함.
7. Epoch와 Batch
- Epoch: 전체 데이터셋을 한 번 학습하는 과정.
- Batch: 한 번의 경사 계산에 사용되는 데이터 단위.
첨부된 문서는 신경망 학습의 전반적인 흐름과 주요 개념들을 체계적으로 설명한다.
특히 최적화 알고리즘과 역전파 과정에 중점을 두고 있다.
러닝 모델의 학습 원리를 이해하고, 다양한 상황에서 적합한 최적화 방법을 선택할 수 있도록 돕는다.
8_dl
1_code
20250212 파일
기본 내용은 이제 skip